渋滞のない社会実現法
友枝 明保
最新記事はこちら
車の流れを記述する数理モデルは主に、偏微分方程式での記述、常微分方程式での記述、セルオートマトンによる記述の3種類がある。自動運転との混交交通を数理的に理解するためには、まず数理科学が交通をどう理解し、分析してきたのかを知る必要がある。
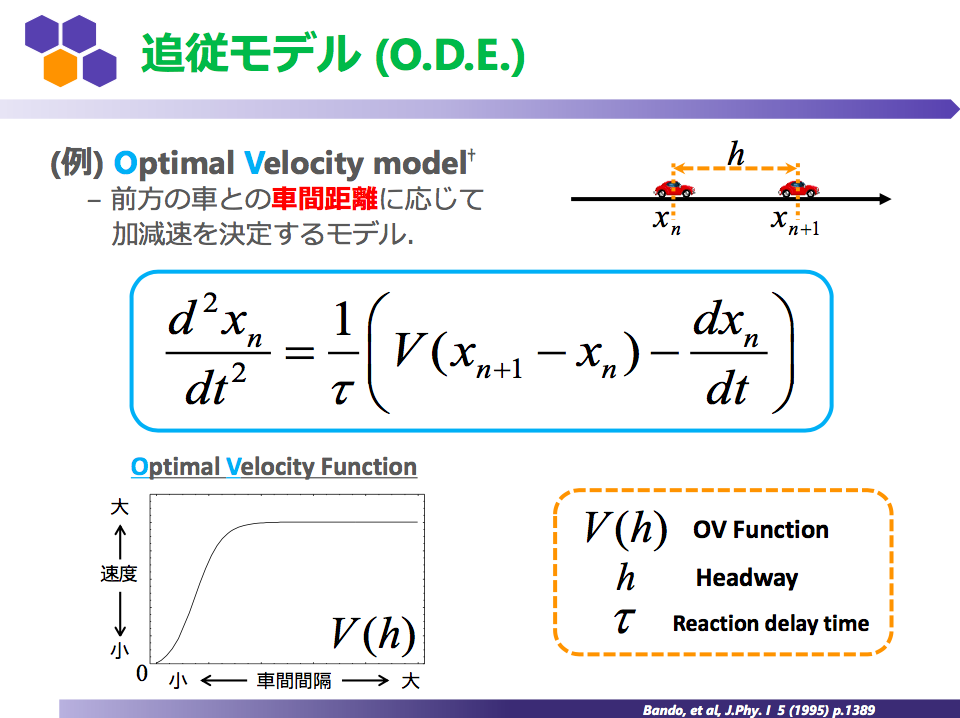
常微分方程式によって記述する「追従モデル」は、前方の車との相互作用を考慮して、個々の車の振る舞いを運動方程式で記述したモデルであり、前方の車の挙動の変化を受けてドライバーがどう加減速するかを表現している。
この立場で作られたモデルの一つが「最適速度模型」(Optimal Velocity model)であり、その解析から渋滞が起きない安定した流れと、渋滞へと変化してしまう不安定な流れとの違いは、ドライバーの反応の速さと車間距離との関係によって決まることがわかる。ドライバーの反応の速さはモデル方程式に含まれる係数τ(タウ)であり、自動運転システムを搭載した車の数が増えることで、反応を早める(τを小さくする)ことができれば、自動車の密度が高くても渋滞は生まれにくくなる。
この動画講義は、全8回を通して、「追従モデル」と「セルオートマトンモデル」と呼ばれる2つの数理モデルから得られる知見や、ドライバーの錯視が運転に与える影響について学び、自動運転との混交交通下での渋滞を数理モデルで考えるための基礎を身につけることを目的としている。
第1章 渋滞の数理科学としての定義
第2章 車の流れを記述する数理モデル1(追従モデル)
第3章 車の流れを記述する数理モデル2(セルオートマトン)
第4章 追従モデルで理解する自然渋滞のメカニズム
第5章 セルオートマトンモデルで見るメタ安定構造
第6章 渋滞吸収運転術―実験による検証
第7章 縦断勾配錯視―道路に潜む錯覚現象
第8章 自動運転との混交交通下での渋滞を数理モデルで考える